اشنکٹبندیی رکاوٹ

    ہر ایک جانتا ہے کہ دو نکات ایک لکیر کا تعین کرتے ہیں ، اور بہت سارے لوگ جنھوں نے جیومیٹری کا مطالعہ کیا ہے وہ جانتے ہیں کہ ہوائی جہاز کے پانچ نکات ایک شنک کا تعین کرتے ہیں۔ عام طور پر ، اگر آپ کے ہوائی جہاز میں میٹر بے ترتیب پوائنٹس ہیں اور آپ ان سب کے ذریعہ ڈگری ڈی کا عقلی منحنی پاس کرنا چاہتے ہیں تو ، اس بازی کے مسئلے کا کوئی حل نہیں ہوسکتا ہے (اگر میٹر بہت بڑا ہے) ، یا لامحدود تعداد میں حل (اگر میٹر بہت چھوٹا ہے) ، یا ایک محدود تعداد میں حل (اگر میٹر ٹھیک ہے تو)۔ معلوم ہوا کہ “ m بالکل ٹھیک ” کا مطلب ہے m = 3 d -1 ( m = 2 لائنوں کے لئے اور m = 5 Conics کے لئے)۔

    اگر ایک مشکل سوال ہے M = 3 ڈی -1، کتنے ڈگری کی عقلی منحنی خطوط ڈی پوائنٹس کو درج؟ آئیے اس نمبر کو N d کہتے ہیں ، تاکہ N 1 = 1 اور N 2 = 1 کیونکہ پچھلے پیراگراف کی لائن اور شنک انفرادیت رکھتے ہیں۔ یہ طویل عرصے سے جانا جاتا ہے کہ این 3 = 12 ، اور 1873 میں زیوتین [ زی ] نے دکھایا کہ این 4 = 620 ہے۔ یہی معاملہ تقریبا دس سال پہلے تک کھڑا ہوا تھا ، جب کونٹسیویچ اور منین [کے ایم ] نے اس نمبر کے لئے ایک خوبصورت تکرار دینے کے لئے کوانٹم کوہومولوجی میں ہم آہنگی کا استعمال کیا تھا۔

    ریئل الجبریک جیومیٹری کے ٹاپولوجیکل پہلوؤں پر ایم ایس آر آئی ونٹر 2004 کے سمسٹر میں تحقیقی موضوعات میں گمنام اصلی اصلی الجبریک جیومیٹری ، اشنکٹبندیی جیومیٹری ، اصلی طیارے کے منحنی خطوط ، اور اصلی الجبریک جیومیٹری کی درخواستیں شامل ہیں۔ یہ سب کچھ اس پرکشیپ مسئلہ نہیں، کے ایک prototypical ہے مسئلہ کے unfolding کہانی میں ایک ساتھ بنے جاتے ہیں enumerative ستادوستی ، دیا واقعات کے حالات کی طرف سے مقرر ہندسی اعداد و شمار گنتی کا فن ہے. یہاں ایک اور مسئلہ ہے: خلا میں کتنی لائنیں چار دی گئی لائنوں کو پورا کرتی ہیں؟ اس کا جواب دینے کے ل note ، نوٹ کریں کہ تین لائنیں ایک دوہری حکمرانی کرنے والے انفرادیت پر مشتمل ہیں۔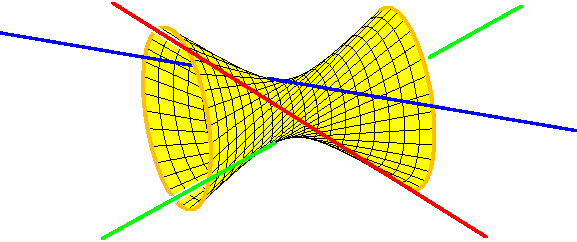

تین حکمران ایک حکم میں مضمر ہیں ، اور دوسرا حکم ان لائنوں پر مشتمل ہے جو دیئے گئے تین لائنوں کو پورا کرتے ہیں۔ چونکہ ہائپر بلڈائڈ کی وضاحت ایک مربع مساوات سے ہوتی ہے ، لہذا ایک چوتھی لائن اسے دو نکات پر پورا کرے گی۔ ان دو پوائنٹس میں سے ہر ایک کے ذریعے دوسرے حکم نامے میں ایک لکیر موجود ہے ، اور یہ وہ دو لائنیں ہیں جو ہماری چار دی گئی لائنوں کو ملتی ہیں۔

اعدادوشمار     جیومیٹری پیچیدہ اعداد پر سب سے بہتر کام کرتا ہے ، کیوں کہ اصل اعداد و شمار کی تعداد اعدادوشمار کی ترتیب پر نہیں بلکہ انحصار کرتی ہے۔ مثال کے طور پر ، چوتھی لائن دو اصل نکات میں ، یا دو پیچیدہ جوڑا پوائنٹس میں ہائپر بولوڈ سے مل سکتی ہے ، اور اس وجہ سے چاروں میں ایک یا دو حقیقی لائنیں مل جاتی ہیں۔ بہت ساری مثالوں کی بنیاد پر ، ہم یہ توقع کرنے لگے ہیں کہ کسی بھی مسئلے کا حل اس کے تمام حل ہو سکتے ہیں [ لہذا ]۔

    اس طرح کا ایک اور مسئلہ طیارے میں 8 پوائنٹس کو جوڑتے ہوئے 12 عقلی منحنی خطوط ہے۔ بیشتر ریاضی دان نوڈل (عقلی) مکعب سے واقف ہیں جو نیچے کی طرف دکھائے گئے ہیں۔ اصلی عقلی مکعب کی ایک اور قسم ہے ، جو دائیں طرف دکھایا گیا ہے۔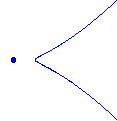دوسرے وکر میں ، دو پیچیدہ اجزاء شاخیں الگ تھلگ مقام پر ملتی ہیں۔ ہم دو تو ن ( T ) قسم کے حقیقی منحنی خطوط کی تعداد ہو جائے T 8 دیا پوائنٹس، پھر Kharlamov اور Degtyarev interpolating [ DK ] سے ظاہر ہوتا ہے کہN ( ) –   N ( ) = 8۔ان کے ابتدائی ٹوپولوجی طریقوں کی تفصیل یہ ہے ۔

    چونکہ اس طرح کے زیادہ سے زیادہ 12 منحنی خطوط ہیں ، N ( ) + N ( ) 12 لیک 12 ، اور اس طرح طے شدہ تعداد میں (0 ، 1 ، یا 2) مکعب کا الگ تھلگ مقام کے ساتھ۔ اس طرح ذیل میں دو مکعب کے چوراہے کے 9 پوائنٹس میں سے کسی 8 کو بازی کرتے ہوئے 12 حقیقی عقلی مکعب ہوں گے۔

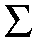
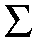
    ویلشنگر [ ڈبلیو ] ، جو پچھلی موسم سرما میں ایم ایس آر آئی کا پوسٹ ڈاک تھا ، نے اس مثال کو نظریہ میں تیار کیا۔ عام طور پر ، ایک حقیقی عقلی طیارہ وکر C کی واحدیت نوڈس یا الگ تھلگ نکات ہیں۔ مراکز کی تعداد کی برابری اس کنندہ نشانی ے ( C )، یا تو 1 یا -1 ہے. ہوائی جہاز میں 3 ڈی -1 اصل پوائنٹس کے پیش نظر ، ویلچنجر نے مقدار کی مطلق قیمت سمجھیs ( C ) ،تمام حقیقی عقلی منحنی خطوط C کی ڈگری ڈی کا جو جمع پوائنٹس کو باہم جوڑتا ہے۔ انہوں نے ظاہر کیا کہ یہ وزن کا مجموعہ پوائنٹس کے انتخاب پر منحصر نہیں ہے۔ ویلشنگر کے اس جارحیت کیلئے W d لکھیں ۔ مثال کے طور پر ، ہم نے ابھی دیکھا کہ W 3 = 8۔

    یہ ایک پیشرفت تھی ، کیوں کہ W D (تقریبا)) اصلی حقیقی الجبرک جیومیٹری میں واقعی غیر معمولی حملہ آور تھا۔ نوٹ کریں کہ W d طیارے میں 3 d -1 اصلی پوائنٹس کے ذریعے حقیقی عقلی منحنی خطوط کی تعداد کے لئے کم حد ہے ، اور W d \ leq N d ۔

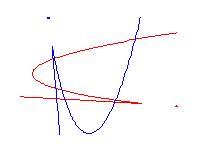
    میخالکن ، جو سمسٹر کا منتظم تھا ، نے اشنکٹبندیی الجبریک جیومیٹری [ ایم آئی ] کا استعمال کرتے ہوئے ڈبلیو ڈی کمپیوٹنگ کی کلید فراہم کی ۔ یہ اشنکٹبندیی سمرنگ کا جیومیٹری ہے ، جہاں زیادہ سے زیادہ اور + حقیقی اعداد پر + کے عمل + اور ضرب کی معمول کی کارروائیوں کی جگہ لیتے ہیں۔ ایک اشنکٹبندیی کثیر المزاقی شکل کا ٹکڑا نما لکیری تقریب ہوتا ہےT ( x ، y ) = زیادہ سے زیادہ ( i ، j ) { x i  +  y j  +  c i ، j }،حساب کتاب معمول ریاضی کی کارروائیوں کے ساتھ ہے اور زیادہ سے زیادہ کی ایک محدود اپسمچی پر قبضہ کر لیا ہے جہاں Z 2 کے exponents میں ٹی اور سی I ، J کی حقیقی تعداد کے جزو عام ہیں ٹی . ایک اشنکٹبندیی کثیرالثانی T ایک اشنکٹبندیی وکر کی وضاحت کرتا ہے ، جو پوائنٹس ( x ، y ) کا سیٹ ہوتا ہے جہاں T ( x ، y ) فرق نہیں رکھتا۔ یہاں کچھ اشنکٹبندیی منحنی خطوط ہیں۔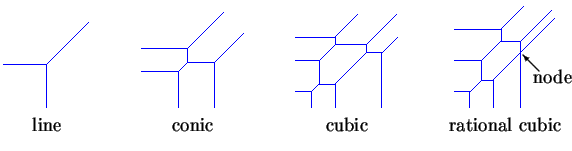

اشنکٹبندیی وکر کی ڈگری مغرب ، جنوب یا شمال مشرقی تینوں سمتوں میں سے کسی ایک میں لامحدود رنگ کی کرنوں کی تعداد ہے۔ اشنکٹبندیی وکر عقلی ہے اگر یہ کسی درخت کا ٹکڑا دار لکیری وسرجن ہے۔ نوڈس میں والینس 4 ہے۔

    میخالکن نے ظاہر کیا کہ صرف 3 D -1 عام نکات کو تقویت بخشنے والی ڈگری ڈی کے بہت ہی عقلی اشنکٹبندیی منحنی خطوط موجود ہیں ۔ اگرچہ اس طرح کے منحنی خطوط کی تعداد پوائنٹس کے انتخاب پر منحصر ہے ، میخالکن نے ہر اشنکٹبندیی وکر کے ساتھ مثبت کثیریت کو منسلک کیا تاکہ وزن کا حص sumہ نہیں ، اور حقیقت میں N d کے برابر ہے ۔ انہوں نے یہ بھی طرف کی لمبائی کے ایک مثلث کے اندر اندر جعلی راستے کی combinatorics لئے ان multiplicities اور اشنکٹبندیی منحنی خطوط کا شمار کم کر د .

    میخالکن نے نقشے پر مشتمل خط و کتابت کا استعمال کیا۔ لاگ 🙁 C * ) 2 -> R 2 کی وضاحت ( x ، y ) | -> (لاگ | x | ، لاگ | y |) ، اور ایک خاص `بڑی پیچیدہ حد ‘ ( C * ) 2 پر پیچیدہ ڈھانچہ کا ۔ اس بڑی پیچیدہ حد کے تحت ، ( C * ) 2 میں 3 D -1 پوائنٹس کو گھسانے والے ڈگری D کے عقلی منحنی خطوط کو ‘پیچیدہ اشنکٹبندیی منحنی خطوط’ کے مطابق بنادیتے ہیں ، جن کی علامت کے نیچے کی تصاویر عام نقطہ نقاط کی تصویروں کو گھیرتے ہوئے عام اشنکٹبندیی منحنی خطوط ہیں۔ اشنکٹبندیی وکر کی ضربT پیچیدہ اشنکٹبندیی منحنی خطوط کی تعداد ہے جو T پر پیش کرتے ہیں ۔

    اصلی منحنی خطوط کے بارے میں کیا خیال ہے؟ اس خط و کتابت کے بعد ، میخالکن نے ہر اشنکٹبندیی منحنی خطوط میں حقیقی ضرب لگائی اور یہ ظاہر کیا کہ اگر دیئے گئے 3 D -1 پوائنٹس کو گھیرنے والے اشنکٹبندیی منحنی خطوط میں اصلی حقیقی ضرب N ہے ، تو پھر 3 D -1 اصلی نکات ہیں جو N اصلی عقلی اعتبار سے گھس جاتے ہیں۔ ڈگری کے منحنی خطوط d . جعلی راستوں کے معاملے میں ایک بار پھر اس حقیقی ضرب کا اظہار کیا گیا۔

    ویلشنگر کے حملہ آور کے بارے میں کیا خیال ہے؟ اسی طرح ، میخالکن نے ہر اشنکٹبندیی وکر (ویلسچنگر کے اشارے کا اشنکٹبندیی ورژن) کے ساتھ ایک دستخط شدہ وزن منسلک کیا اور یہ ظاہر کیا کہ اس سے متعلق وزن اشتہار ویلشیچنگر کے ناگوار کے برابر ہے۔ پہلے کی طرح ، اس اشنکٹبندیی دستخط شدہ وزن کا استعمال جاٹوں کے راستوں کے لحاظ سے کیا جاسکتا ہے۔

    ایم ایس آر آئی کے سمسٹر کے دوران ، استن برگ ، خرلاموف ، اور شسٹین [ آئی کے ایس ] نے ویلشنگر کے ناگوار ہونے کا اندازہ لگانے کے لئے میکالکن کے نتائج کا استعمال کیا۔ انہوں نے یہ ظاہر کیا کہ W d \ geq d ! / 3 ، اور یہ بھیلاگ ان W D  = لاگ ان ن د  +  O ( د )، لاگ ان ن د  = 3 ڈی تبا د + O ( D ).اس طرح کم سے کم لوگرتھمک طور پر ، ہوائی جہاز میں 3 ڈی -1 اصل پوائنٹس کو گھسانے والی ڈگری ڈی کے بیشتر عقلی منحنی خطوط حقیقی ہیں۔

    نچلے حد کے اس رجحان کی دو اور مثالیں بھی موجود ہیں ، جن میں سے پہلی میں ویلچنگر کے کام کی پیش گوئی کی جاتی ہے۔ فرض کریں کہ ڈی مساوی ہے اور ڈبلیو ( زبانیں ) کو ڈگری k ( d – k +1) کا حقیقی بہ کثیر بننے دیں ۔ تب ایریمینکو اور گیبریلوف [ ای جی ] نے ظاہر کیا کہ وہاں اصلی کثیر الجماعات موجود ہیں f 1 ( s )، …، f k ( s ) کی ڈگری ڈی جس کا Wronski تعین کرنے والا W ( s ) ہے۔ اصل میں، وہ کی تعداد پر ایک کم پابند ثابت ہوا Kمتعدد متعدد تکمیلات۔ اسی طرح ، جبکہ ایم ایس آر آئی میں ، سوپرونوفا اور میں [ ایس ایس ] نے پوزوں سے وابستہ ویرل کثیر الثانی نظام کا مطالعہ کیا ، جس سے یہ ظاہر ہوتا ہے کہ پوزیٹ کے علامت عدم توازن سے حقیقی حل کی تعداد نیچے جکڑی گئی ہے۔ قابل قدر مسائل کی ایسی کم حدیں ، جو حقیقی حلوں کے وجود کو ظاہر کرتی ہیں ، درخواستوں کے ل for اہم ہیں۔

    مثال کے طور پر ، اپریل 2004 میں جیومیٹرک ماڈلنگ اور اصلی الجبریک جیومیٹری سے متعلق ایم ایس آر آئی ورکشاپ میں ایک شام بیئر پر یہ کہانی سنائی گئی تھی۔ ایک شریک ، شوچو ، نے سمجھا کہ نتیجہ مکعب کے لئے ڈبلیو 3 = 8 نے بتایا کہ اس کا طریقہ ہمیشہ تیار کیوں ہوتا ہے کام کرنا. قوس پر ایک حقیقی عقلی کیوبک انٹرپولٹنگ 8 کے ذریعہ کسی منحنی خط کے قریب قریب پیرامیٹریائزیشن کی گنتی کرنے کے لئے یہ الگورتھم تھا۔ یہ ایسے حالات تلاش کرنا باقی ہے جو کسی حل کے وجود کی ضمانت دیتا ہے جو قوس کے قریب ہے۔ اس کا حل صرف ایک ایم ایس آر آئی پوسٹڈاک فیدلر لی ٹوزا نے کیا جس نے ڈگری 9 کے ہوائی جہاز کے منحنی خطوط کی درجہ بندی کرنے میں مدد کرنے کے لئے 8 پوائنٹس کی باہمی مداخلت کرتے ہوئے مکعب کا مطالعہ کیا تھا۔

کتابیات

[ڈی کے]A. I. Degtyarev اور V. M. Kharlamov ، اصلی الجبراicک قسموں کی ٹوپولوجیکل خصوصیات: روکھلن کا راستہ ، اوسپیکھی میٹ۔ نوک 55 (2000) ، نہیں۔ 4 (334) ، 129–212۔
[ای جی]اے ایریمینکو اور اے گبرییلوف ، اصلی ورونسکی نقشوں کی ڈگری ، مجرد کمپیوٹ۔ جیوم۔ 28 (2002) ، نہیں۔ 3 ، 331–347۔
[IKS]I. Itenberg ، V. Kharlamov ، اور E. Shustin ، ویلشیچنگر اور Gromov-Witten حملہ آوروں کی لوگرتھمک مساوات ، arXiv: ریاضی.اگ / 4040/188 ۔
[KM]ایم کونٹسیویچ اور یو۔ منین ، گروموف وٹین کلاسز ، کوانٹم کوہومولوجی ، اور گنتی جیومیٹری ، کام۔ ریاضی جسمانی 164 (1994) ، نہیں۔ 3 ، 525–562۔
[مجھے]جی میخالکن ، R 2 میں ارقماتی اشنکٹبندیی الجبریک جیومیٹری ، arXiv: math.AG/0312530 ۔
[ایس ایس]ای سوپرونوفا اور ایف۔ سوٹل ، نچلے حدود حقیقی حل کے لئے کثیر الثانی سسٹمز کو کم کرنا ، arXiv: math.AG/0409504 ۔
[تو]ایف. سوٹائل ، گمنام اصلی الجبریک جیومیٹری ، الگورتھمک اور مقداری اصلی الجبریک جیومیٹری (پِسکٹا وے ، این جے ، 2001) ، ڈی آئی ایم اے سی ایس سی۔ مجرد ریاضی نظریہ کمپیوٹ سائنس ، جلد 60 ، عامر۔ ریاضی ساک. ، پروویڈنس ، RI ، 2003 ، صفحہ 139–179۔
[ڈبلیو]J.-Y. ویلچنگر ، حقیقی محققانہ جیومیٹری میں حقیقی عقلی علامتی 4 متعدد گنا اور نچلے حدود کے متغیر ، سی آر میتھ۔ اکاد۔ سائنس پیرس 336 (2003) ، نہیں۔ 4 ، 341–344۔
[وہ]H. جی. زیوتین ، المندلیج ایجینسکابر وید سسٹیمر اے ایف ہوائی جہاز کرور ، ڈانسکے وڈینسکابرنس سیلسکبس اسکیفٹر ، نیٹورویڈنسکابلیگ اور میتھیمتسک ، افف۔ 10 بی ڈی چہارم (1873) ، 286–393۔

ہم اپنے ایڈیٹر سلویو لیوی اور ایم ایس آر آئی ممبروں کا جن کا کام ہم بیان کرتے ہیں شکر گزار ہیں۔

نیشنل سائنس فاؤنڈیشن کے ذریعہ کیریئر DMS-0134860 ​​اور DMS-9810361 (MSRI کو مالی اعانت فراہم کرنے) ، اور کلی میتھیمیٹک انسٹی ٹیوٹ کی معاونت ہے۔

آخری بار نظر ثانی شدہ: پیر اپریل 23 15:33:30 سی ای ایس ٹی 2018

Frank Sottile
9 October 2004, College Station, Texas.